February'2001
this paper is a part from AI- Project

     In this paper we are going to find out what is an arbitrary world and when two worlds are indistinguishable. Also, we are going to think whether the world is determined or not. We are going to ask ourselves how would AI cope, without knowing the world it got into. We are going to see that the way for understanding the world is the building of a correct model.

 
       This paper is the sequel of "AI - What is this" (ed. 11/2000). We said there that we want to create a device which in an arbitrary world will cope not worse than a human being. Let us think what is an arbitrary world and how our device would cope in such world. We are going to ask ourselves how many are the possible world’s states and when two worlds are indistinguishable?
       We said that an arbitrary world is an arbitrary function World(s, d), the arguments of which are the world’s state and the influence that our device has on the world. The result of this function is the world’s new state. We said that the device works out finite information (m bits), i.e. the possible influence actions towards the world are finite (2^m).
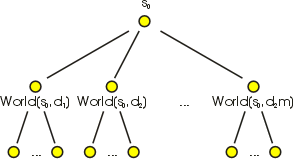
       Let us have an arbitrary world. We are going to build the tree of the attainable world’s states. An attainable world’s state will be the one that can be reached by our device (or the one that the device can bring the world to). In the tree’s root we are going to place the state s₀. This world’s state will be reached at the moment of birth. Inheritors of s₀ will be the states World(s₀, d_i) where d_i runs through all possible actions (as we have already said, they are a finite number). These states can be reached in a moment one (if the action in moment zero was the respective one).
       By analogy, we define the inheritors of the inheritors and so on. We get an infinite tree with countably many knots. We will call this tree the tree of the attainable states.

       From the tree of the attainable states we can easily get another tree, which we will call the tree of the world. This will be the same tree but at each knot instead some state (s_i) we will juxtapose View(s_i), i.g. instead the respective world’s state we will juxtapose the information the device gets as an entrance when it is in that state (what it sees). Why did we call this tree with the pretentious name tree of the world? It is because that if two worlds have the same tree of the world then they are absolutely indistinguishable from the point of view of the device. No matter what experiment it would carry out, it would get the same result in both worlds because with the same sequence of actions it would see the same things.

 
       Now we are ready to answer the question how many the world’s states are. They can be arbitrary many, but because only the attainable ones matter we can safely consider that the others do not exist. It means that if we throw out the unattainable states from a world, we will get a world indistinguishable from the given one. The newly obtained world will have no more than countably many states. 
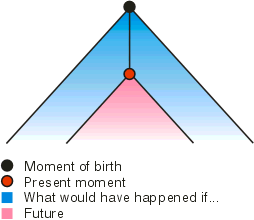
       What is the life of our device? This is a path in the tree of the world, starting from the root View(s₀). This path is potentially infinite but at a given moment t of its life the path has length t. What does our device know at the moment t? Up to this moment it knows only its own life path, the other knots are - what would have happened if it would have done another thing or what will happen in future. All these are things that our device does not know and only can suppose about them.

       That is to say, our device is at the moment t of its life and its task is to understand the world, to understand the principles that make it move. This understanding of the world is necessary for it to be able in future to choose its way better and to get a better mark for its actions. Well, the understanding of the world is important, but how it can be done, how from a finite path in a infinite tree a whole tree can be built.
       The latter (to be built a whole tree) is a too ambitious task. This means the world to be fully understood. If you understand fully the world you live in, you will not need to carry out experiments, because you will know the result you will get. For example, you will not have to look for your things, because you will already know where they are, even when you throw dice you will know what will the result be, also you will know the lottery numbers. As you can see, you do not know fully the world you live in and it is not sensible for us to hope our device to achieve such a result. We can have full knowledge of the world only in very simple worlds, but even there, even if we have a model, giving us a full description of the world, we can never be sure that this is a correct model. This model could have proved itself million times, but we do not have guarantees that in the million and first one it will not mislead us.